[聚集行]【ArcGIS教程】（75）空间自相关分析

内部空间自有关预测——以高/低控制点财务报表为例

内部空间自有关预测

地质学第三运动定律：（Toblers First Law或是Toblers First Law of Geography）Everything is related to everything else, but near things are more related to each other.（任何表达方式都是与其它表达方式有关的，或是说相似的表达方式关连更密切）

乱数原产电荷原产控制点原产

（1）自上而下内部空间自有关

Moran’s I 富勒成分股Geary’s CGetis’s G

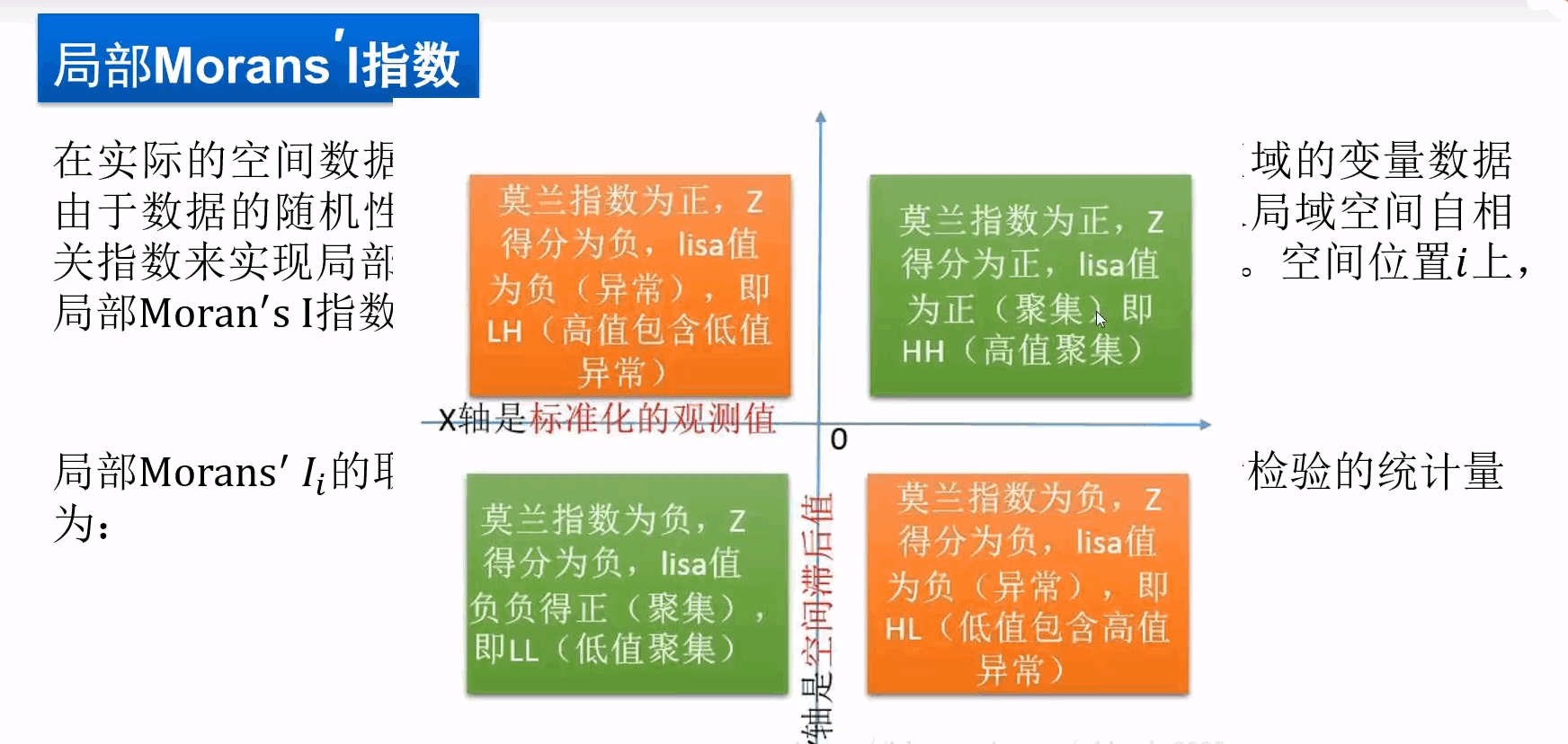
(2)局部性内部空间自有关

局部性Moran’s IGetis’s-Ord Gi*Moran’s I成分股

Moran’s I成分股

局部性Moran’s I成分股

热点预测

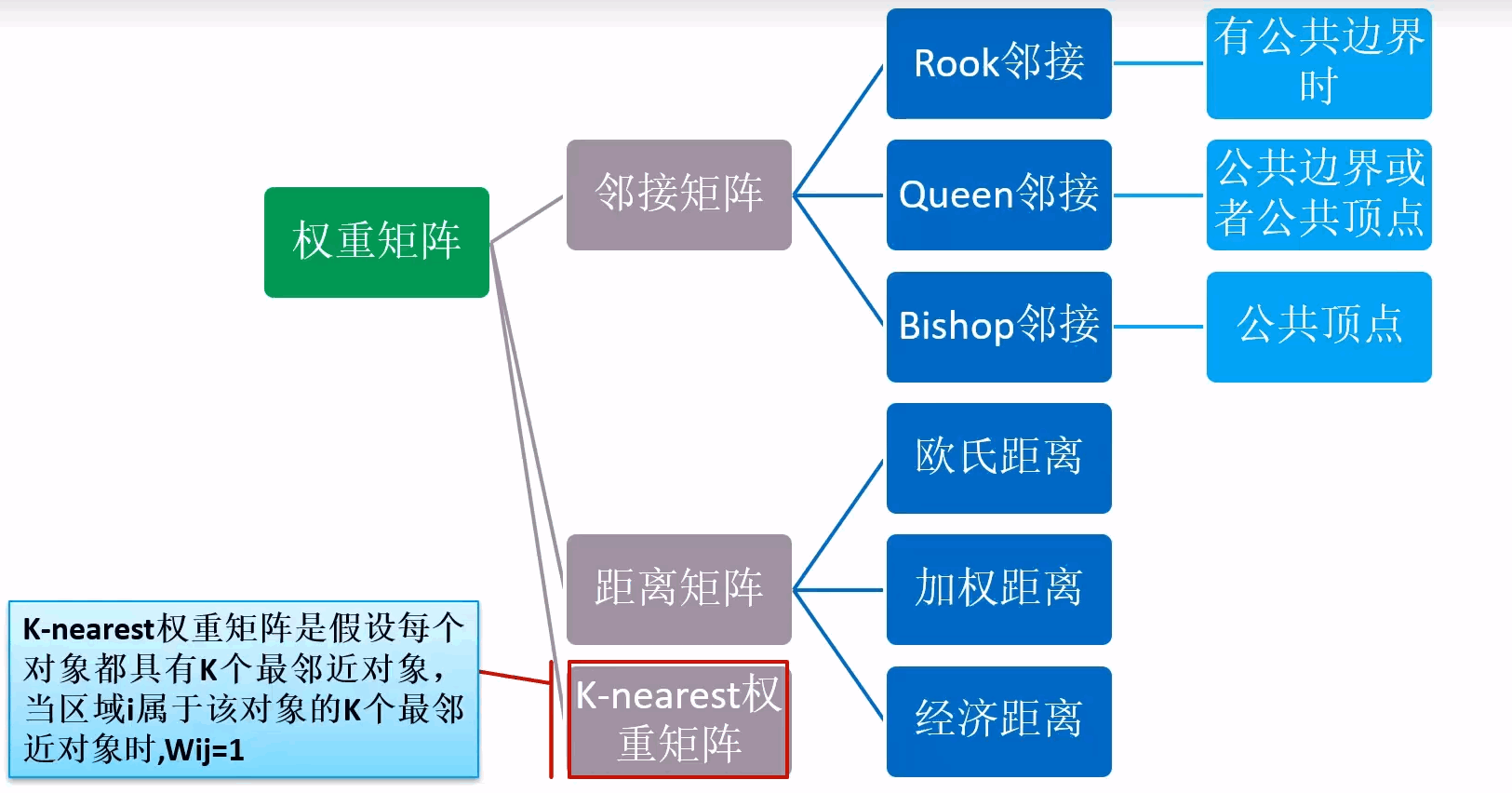
权重矩阵

权重矩阵

我们这里使用的是GDP数据（人均GDP）

查看属性表

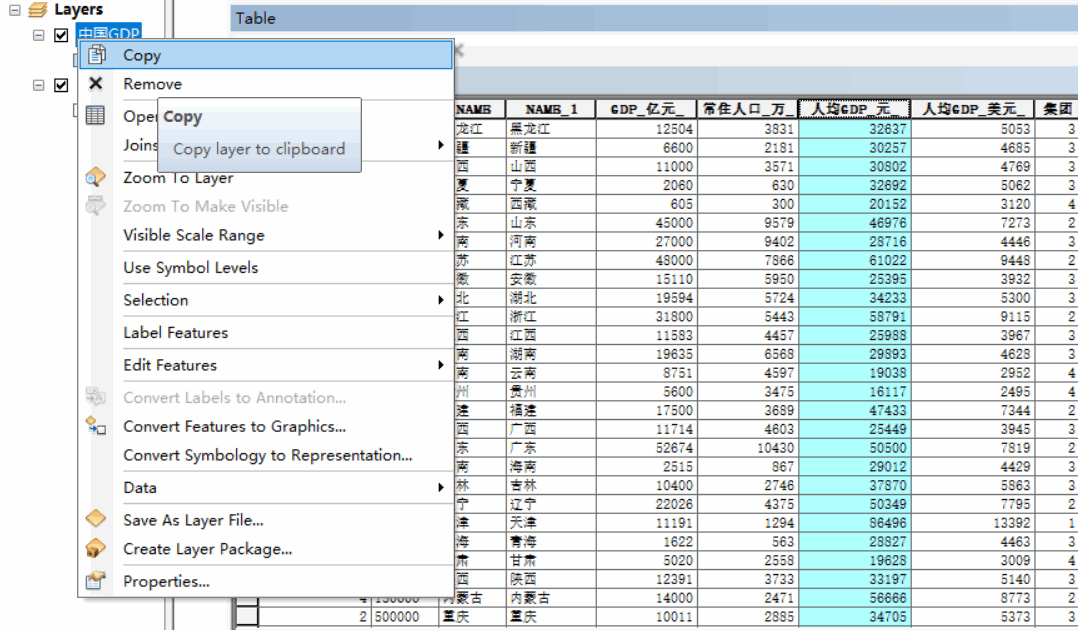
运行ArcToolbox，打开【内部空间统计工具】，选中【预测模式】里面的【内部空间自有关（富勒成分股）】工具，进行参数设置。输入字段选择人均GPD；勾选生成财务报表工具；内部空间关系的概念化选中如图；标准化选中ROW（行）

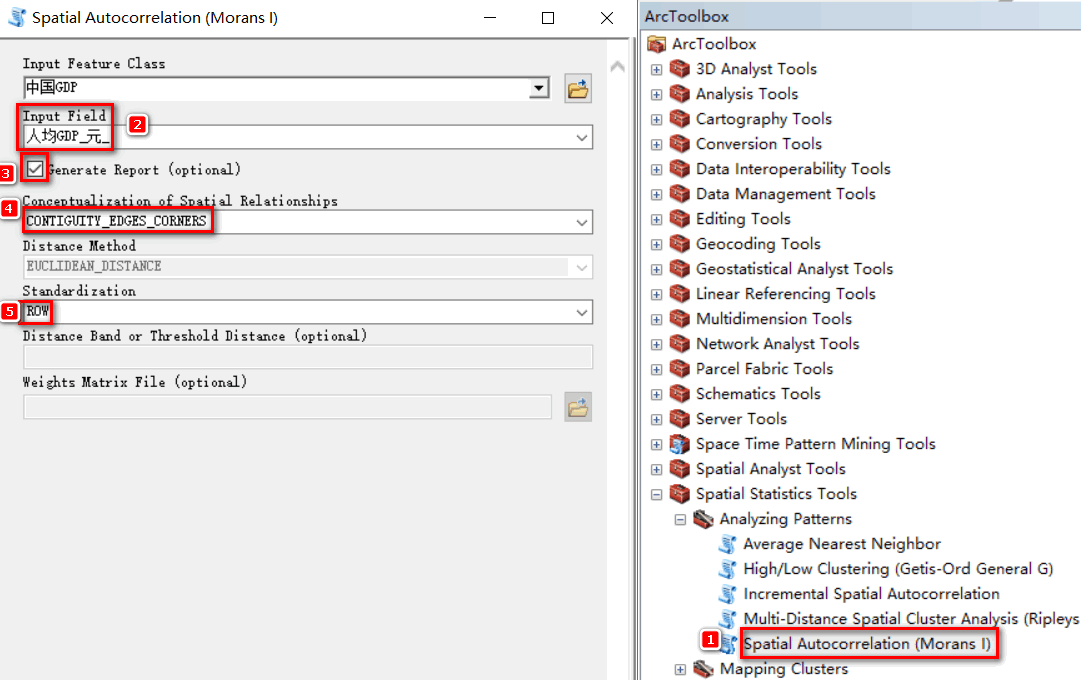
运行完成后在ArcMap里面并不会生成要素，我们打开ArcGIS的默认文档存储路径

如下，打开生成的富勒成分股财务报表

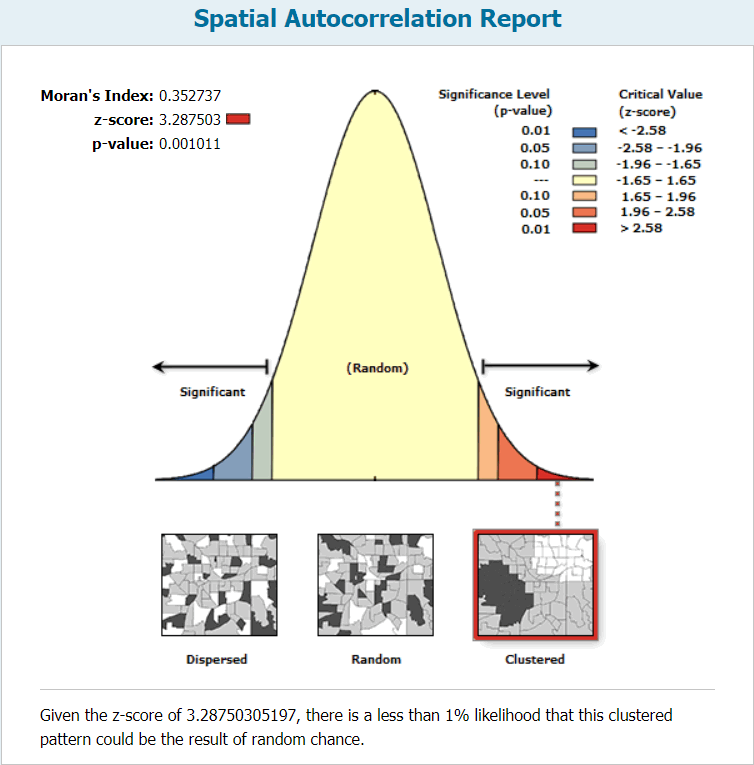
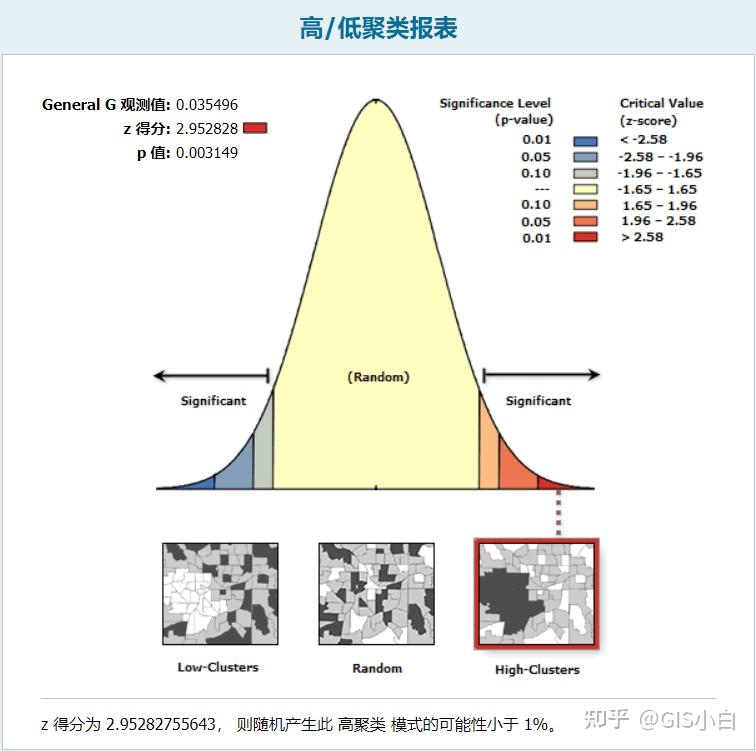
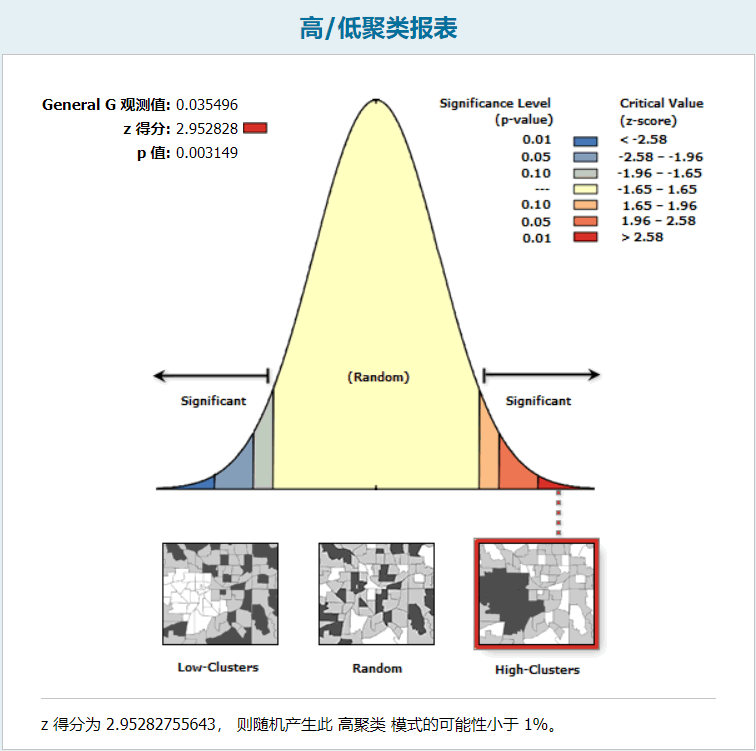
当Z-score值>2.58时则乱数产生此 高控制点 模式的可能性要<1%,即GPD原产具有一定的内部空间集聚性

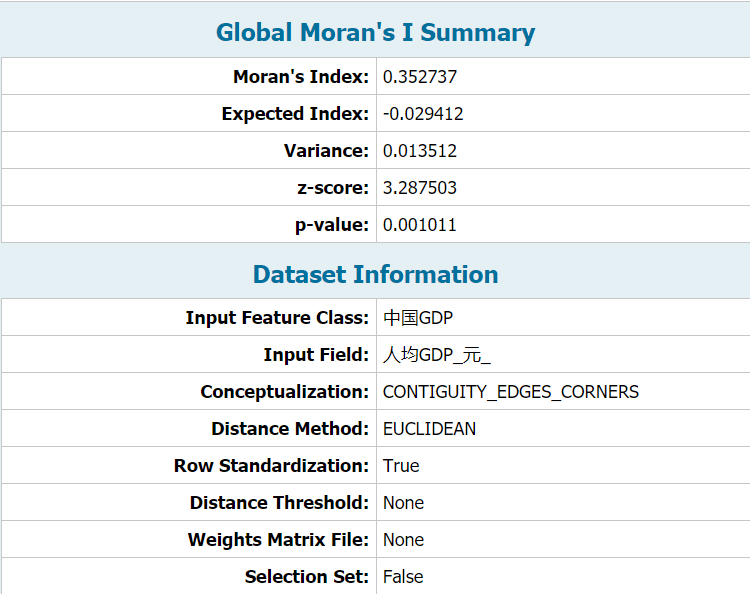
内部空间自有关工具返回五个值：Morans I 成分股、预期成分股、方差、z 得分及 p 值。

在给定一组要素及有关属性的情况下，该工具评估所表达的模式是控制点模式、离散模式还是乱数模式。使用 z 得分或 p 值指示统计显著性时，如果 Morans I 成分股值为正则指示控制点趋势，如果 Morans I 成分股值为负则指示离散趋势。

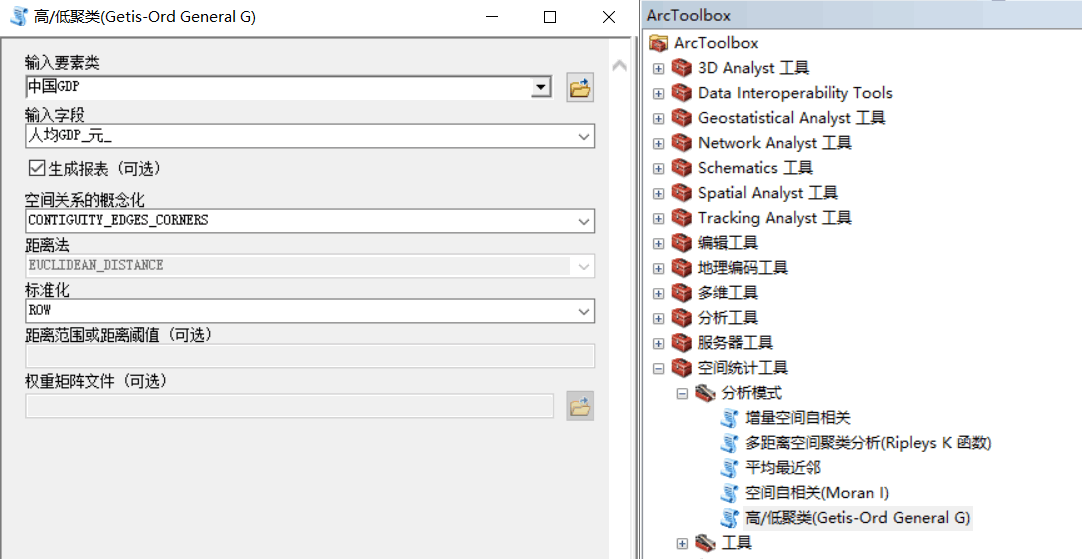
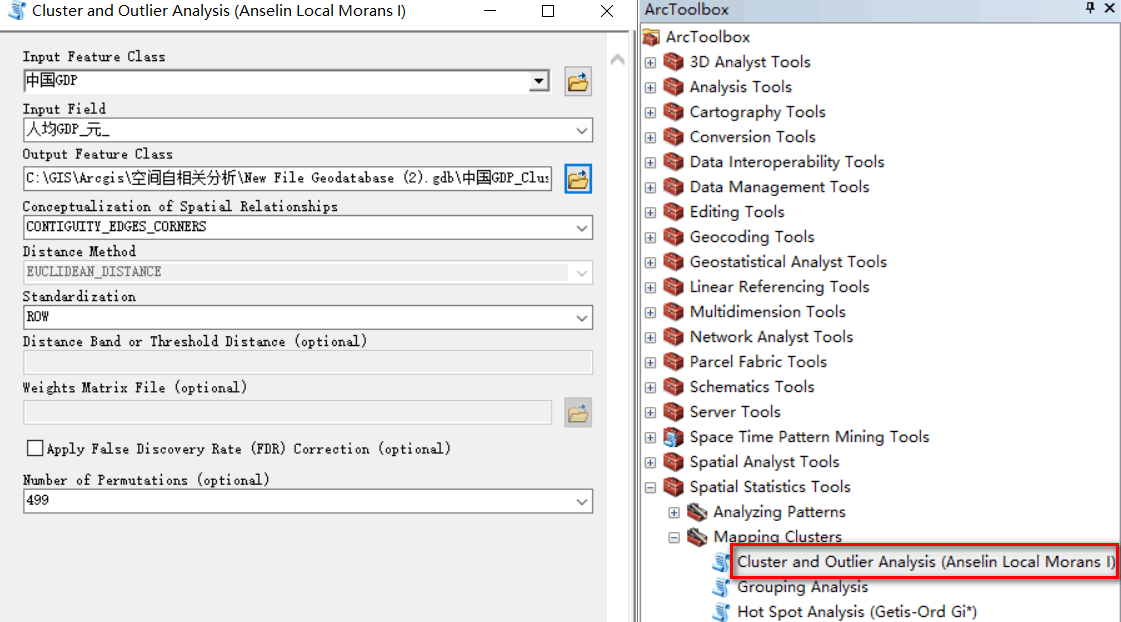
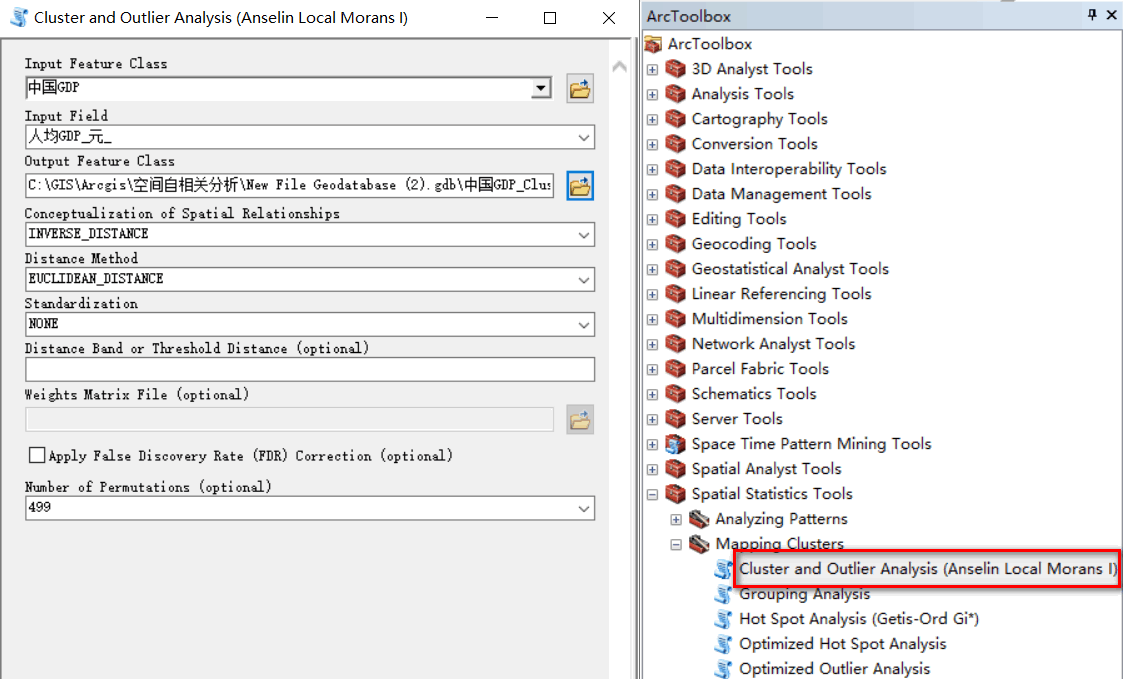
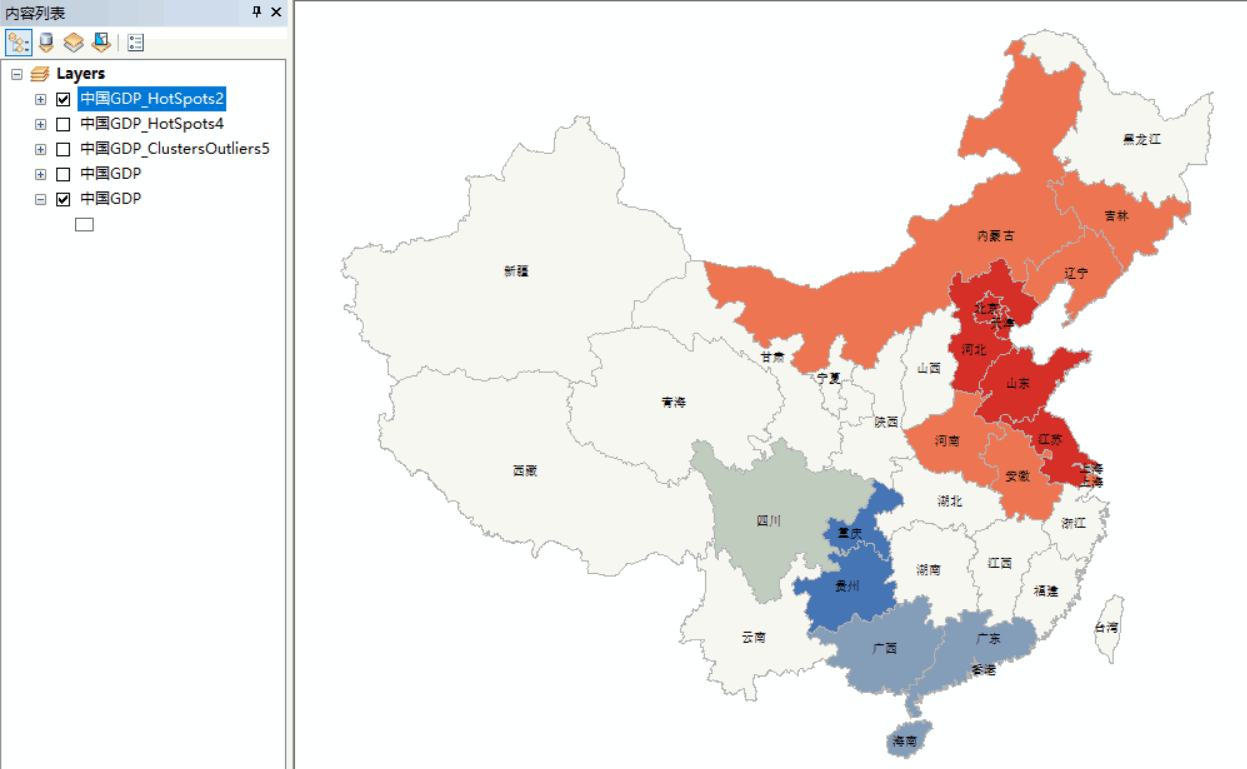
运行ArcToolbox，打开【内部空间统计工具】，选中【控制点原产制图】里面的【控制点和异常值预测】工具，进行参数设置。输入字段选择人均GPD；内部空间关系的概念化选中如图；标准化选中ROW（行）

生成图层如下

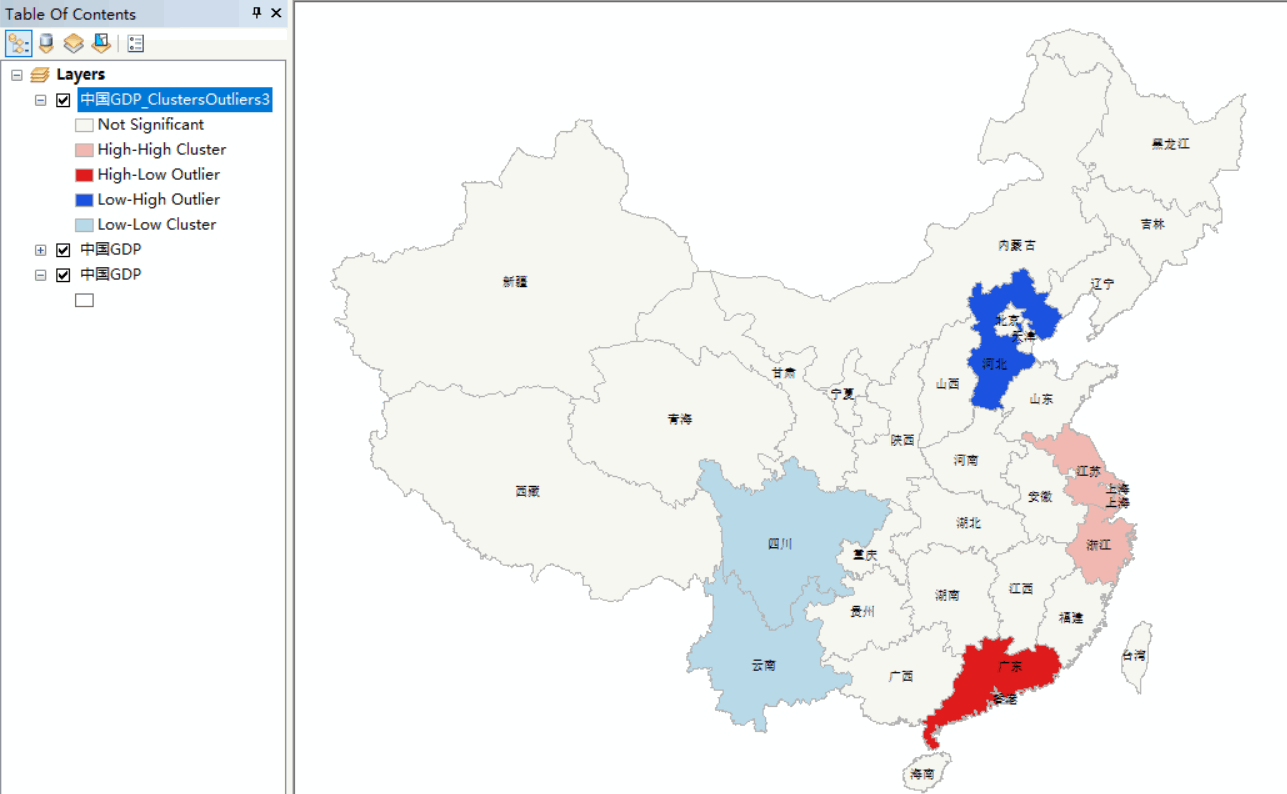
在左边可以看到，Not Significant表示没有显著性；High-High Cluster表示高高集聚，即本身的人均GDP较高，邻近区域的人均GDP也相应较高；High-Low Outlier表示多寡集聚，即本身人均GDP较高，临近区域的GDP较低；Low - High Outlier表示低高集聚，即本身人均GDP偏低，临近区域人均GDP较高；Low - Low Cluster表示低低集聚，即本身的人均GDP较低，邻近区域的人均GDP也相应较低

当然在参数设置时我们也可以默认

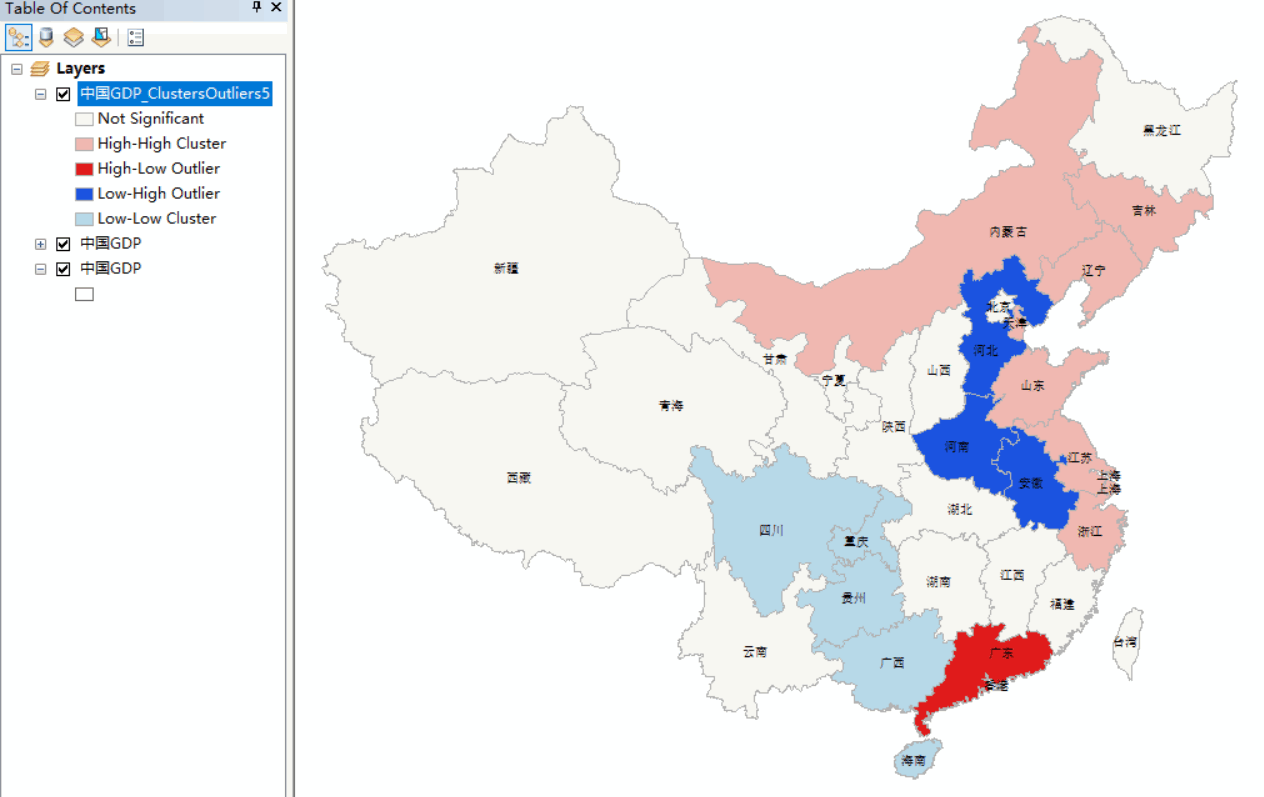
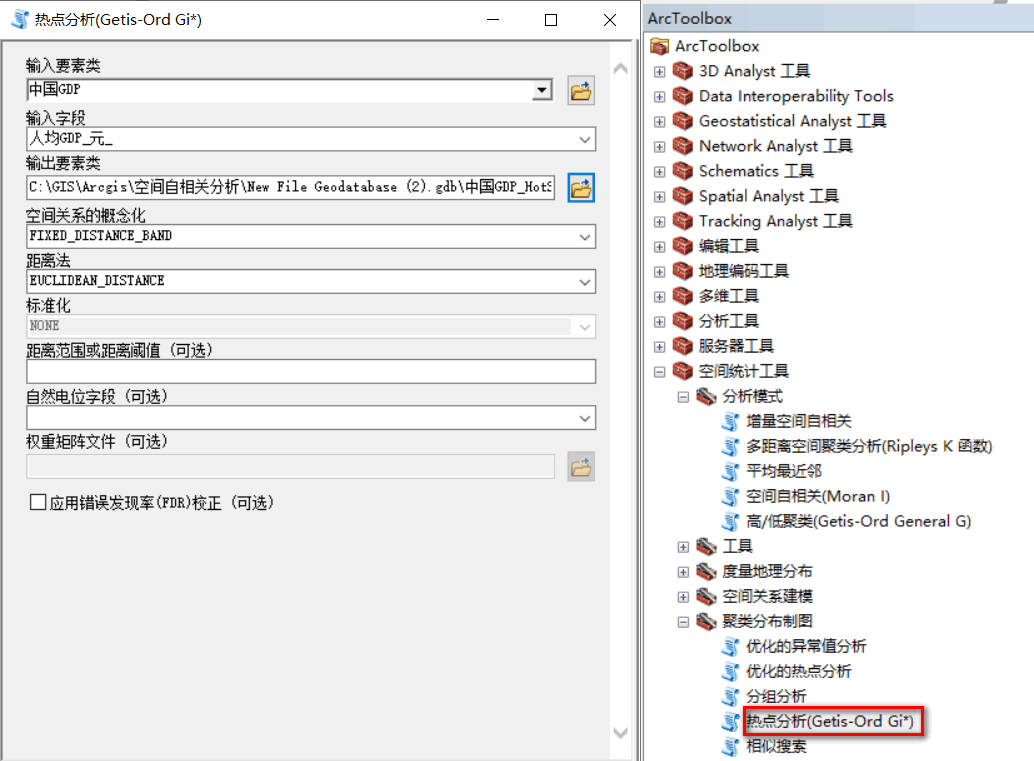
运行ArcToolbox，打开【内部空间统计工具】，选中【控制点原产制图】里面的【冷热点预测】工具，进行参数设置。这里默认即可

为何会得到大于 1.0 或小于 -1.0 的 Morans I 成分股？

通常，Global Morans I 成分股介于 -1.0 到 1.0 之间。只有对权重进行了行标准化时才会这样。如果未对权重进行行标准化处理，则成分股值可能会落在 -1.0 到 1.0 的范围之外，这表示参数设置有问题

何时采用自上而下富勒成分股（Global Morans I），何时采用局部性富勒成分股（Local Morans I），以及，两者有何区别？

富勒成分股分为自上而下富勒成分股（Global Morans I）和局部性富勒成分股（Local Morans I），前者是Patrick Alfred Pierce Moran于1950年提出，用来衡量内部空间自有关程度的度量；后者是美国亚利桑那州立大学地理与规划学院院长 Luc Anselin 教授在1995年提出的。

通常情况，先做一个地区的自上而下成分股，自上而下成分股只是告诉我们内部空间是否出现了集聚或异常值，但并没有告诉我们在哪里出现。换句话说自上而下MoranI只回答Yes还是NO；如果自上而下有自有关出现，接着做局部性自有关；局部性MoranI会告诉我们哪里出现了异常值或是哪里出现了集聚，是一个回答Where的工具。

富勒成分股参考

链接：

提取码：MGIS